実装は無駄になりましたがどんなポリゴンが悪さをするかの知見は無駄ではなかったと信じています(強がり)。
修正できる既存ノードの発見
まず前回の様な一部が縮退している Primitive の修正なんですが、既存ノード Divide で一発KOでした。
問題となる Primitive を再現する Detail Wrangle コード
以下のコードを Detail Wrangle で実行すると
vector add_Ps[] = array(set(-1, 0, 0),set(-1, 4, 0),set( 1, 4, 0),set( 1, 0, 0),set( 2, 0, 0));int add_pts[];foreach (vector add_P; add_Ps){append(add_pts, addpoint(0, add_P));}addprim(0, "poly", add_pts);
問題の縮退 Primitive を再現できます。Point 4 が縮退しています。
さらに難しいケースが見つかった
ひとつの Vertex の消去だけでは解決しないケースが見つかりました。
float h = 0.5;float w = 0.5;float mid_h = chf("mid_h");vector add_Ps[] = array(set( 3*w, 0, 0),set(-3*w, 0, 0),set(-3*w, h, 0),set(-2*w, h*0.75, 0),set(-1*w, h, 0),set(-1*w, mid_h, 0),set( 0, 0, 0),set( 1*w, mid_h, 0),set( 1*w, h, 0),set( 2*w, h, 0));int add_pts[];foreach (vector add_P; add_Ps){append(add_pts, addpoint(0, add_P));}int prim = addprim(0, "poly", add_pts);setprimgroup(0, "dummy_grp", prim, 1);
(最後の行のグループ設定は後で説明します。)
これに前述と同じ Divide ノードを繋げると以下のようになります。
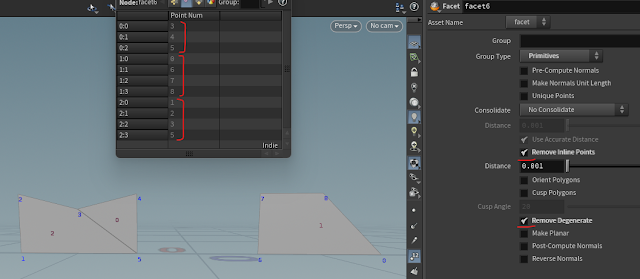
さらに以下の設定の Facet ノードを繋げるとこうなります。
ただし左側が二つの Primitive に分かれてしまっているので最後にこれの対処をします。
 |
| Facetノードまではこのように残っているグループ情報が… |
 |
| Divideノードでエッジを消すと消えてしまう |
これへの対処として Divide ノードの代わりに Labs Dissolve Flat Edges ノードを使います。
同時に来ますので、For-Each Primitive で囲って最後に Fuse させます。









0 件のコメント:
コメントを投稿