2023年7月9日日曜日

Houdiniポリゴン専門医への道002 - "Crossed Boundary Unshared Edges" の解消

自分は Houdini でプロシージャルモデリングをしているとき、Unshared Edge を使うことが多いです。Unshared Edge とは Group ノードを下図のように指定すると得られるエッジグループで、他の Primitive と共有（シェア）していないエッジを抽出してくれるので、普通は図のようにメッシュの外側のエッジが選択されます。

unshared edge グループの作り方

しかしこのような外側のエッジをグループ化しようとしても失敗するケースがあります。
例えば Labs Lot Subdivision を使う場合です。



Grid に Labs Lot Subdivision を繋げると
シンプルな Grid が
良い感じに分割されます

しかしこの分割後の Primitive に対して unshared edge のグループを作って見ると以下のようになります。
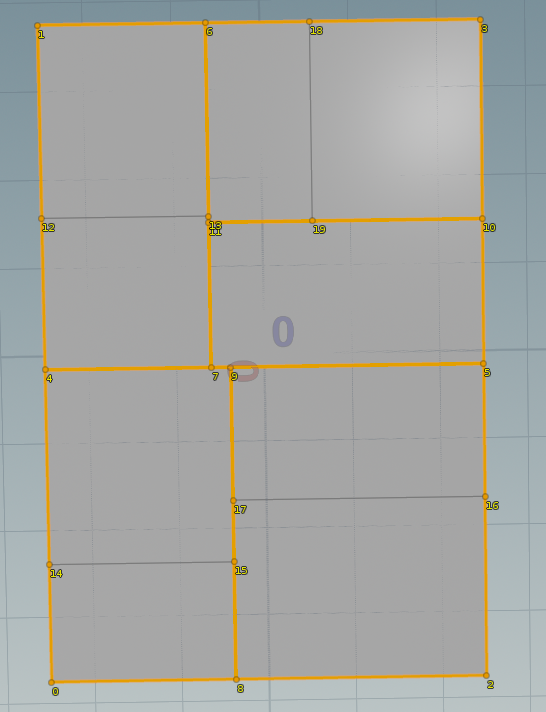unshared edge グループには
外周のエッジ以外のエッジも含まれてしまっている
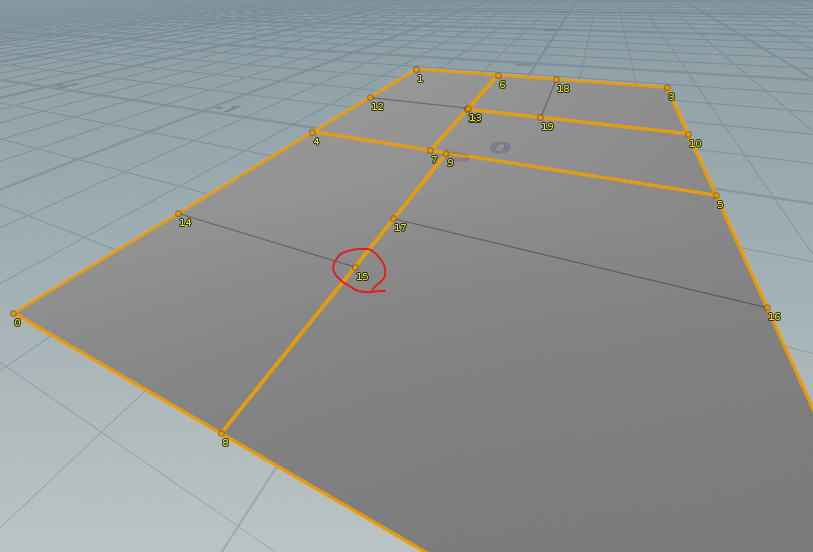どうなっているかを確認するために
一つの Point を選択してY軸方向に動かして見ます。
動かすとこんな感じになっており、
間に穴が開いていることが分かります。
これが Unshared Edge として選択されてしまう原因です。
Boxに対しても同じように Unshared Edge が
沢山出来てしまっていることがわかります。

以上が Unshared Edge として検出されてしまう原因の説明です。
注意したいのは、Labs Lot Subdivision の実装に欠陥があるのではなく、そういう方針での実装なのだろうと思います。実際に用途としてはこの結果のように別々の Primitive として生成されて欲しい時も勿論ありますので。一方でやはり繋がっていて欲しいときもあります。

よってこの繋がっていない分割後のメッシュに対して処理を実装することで
Unshared Edge にならないようにするのが今回のテーマです。

ちなみに…

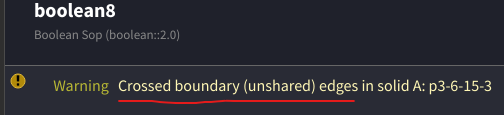
この繋がっているようでいて実は穴が開いている、という状態に対して Boolean をすると
以下の様な警告が出ます。この警告から Crossed Boundary Unshared Edges と呼んでいるんだな、と察しました（違ってたらスイマセン）

ちなみにその２

実はこの状態のときに Boolean Union を自分自身に対してのみ適用すると塞いでくれるケースも多いです。ただ自分の遭遇したユースケースでは塞いでくれないこともあったため、今回の実装を実際には使っています。
メンドクサイ場合は Boolean を試してみるのもおススメです。

アルゴリズムを考える

まずは下の図の Point 111 について考えてみます。
この Point 111 は一見すると３つの Primitive 7, 42, 43 の構成員に見えますが…
Geometry Spreadsheet で確認すると、Primitive 42, 43 には Point 111 が
所属しているのに対して、Primitive 7 には Point 111 が存在しません。

このように Primitive 7 にとっては Point 111 は赤の他人なのです。
これを Primitive 7 の家族に含めるように繋げてやれば、この部分の Unshared Edge を消すことが出来ます。

それではアルゴリズムを考えてみましょう。
具体的に今回の用途に使える道具は以下の３つです。
  1. Point は自分が所属している Primitive のリストを知ることが出来る(pointprims 関数)
  2. Point の位置に近い Primitive を探すことが出来る(xyzdist 関数)
  3. 線分と点の距離を求めることが出来る(ptlined 関数)
以上を踏まえると、アルゴリズムは以下のようになります。

a．全ての Point に対して

  1. まず xyzdist をして Primitive を探す前に、自分が既に所属している Primitive を pointprims 関数で配列として受け取る
  2. xyzdist の検索結果にその所属済みの Primitive がヒットしないように、グループ指定文字列を作成する。
    • 既に所属している Primitive 42, 43 は xyzdist の検索から
      除外し、Primitive 7 だけが探せるようにしたい

  3. グループ指定文字列を作成して xyzdist を行うと Primitive 7 が見つかる。
  4. Primitive 7 のどれかの Edge の上に自身の Point が乗っているかどうかを判定する
    • 例えばこの図のように、Point 0 が xyzdist をした結果
      Primitive 2 が見つかったとしても、その Edge の上に
      乗っていなければ追加してはいけません。
  5. Edge の上に乗っているなら見つけた Primitive に自身の Point Number を教えてあげる

b. 全ての Primitive に対して

  1. 前段の Point 処理から教えてもらった追加すべき Point Number が無ければ何もしない
  2. 存在するならば、追加すべき Point 全てに対して、どの Edge に乗るか調べる
  3. 乗る Edge が分かったら Point 配列のその適切な位置に追加すべき Point を追加する
  4. 全ての追加すべき Point を追加し終わったら、Primitive を新しく作り直し、元の Primitive を削除する

VEXプログラム

以上のアルゴリズムを実行する処理の具体的な説明です。

１．まずは全ての Primitive に対して（つまり Primitive Wrangle でのコード）、追加分の Point 番号を格納する先である空の配列をアトリビュートとして用意しておきます。
（rcbue は Remove Crossed Boundary Unshared Edges の頭文字） 

// Prepare an empty array of attributes to store.
int append_pts[];
setprimattrib(0, "rcbue__append_pts", @primnum, append_pts);

２ー１．次に Point Wrangle にて自分が所属する Primitive を除外した xyzdist を実行するために Group 文字列を作ります。
作成したいGroup文字列は 「* ^プリミティブ番号 ^プリミティブ番号…」という記述になります。* は全てにマッチ、^ は直前のグループから除外するものを指定、という意味です。（参考：https://www.sidefx.com/ja/docs/houdini/model/groups.html）

        int pt_prims[] = pointprims(0, @ptnum);
        string prim_grp = "*";
        // Exclude primitives to which the Point already belongs from the search.
        foreach (int pt_prim; pt_prims)
        {
            prim_grp = sprintf("%s ^%s", prim_grp, pt_prim);
        }

２ー２．xyzdist を実行してヒットした Primitive 番号とそのヒット位置を求めます。

// Search for the nearest primitive to which the Point does not belong.
int prim = -1; vector uvw;
float dist = xyzdist(0, prim_grp, @P, prim, uvw);
vector hit_P = primuv(0, "P", prim, uvw);

２－３．見つけた Primitive の Edge に乗っているか確認し、乗っていたら Primitive の追加すべき Point 配列アトリビュートに "append" モードで追加します。
Primitive の Edge の上に乗っているか判定する関数 dgfx_Pos_Is_On_Primitive_Edges の詳細の説明は省きますが後程紹介するリポジトリで実装内容を見ることが出来ます。

// Determines if the specified position P is
// on the edge of the primitive found by xyzdist.
if (!dgfx_Pos_Is_On_Primitive_Edges(0, prim, hit_P, eps))
{
    prim = -1;
}
else
{
    setprimattrib(0, "rcbue__append_pts", prim, @ptnum, "append");
}
３．最後の Primitive Wrangle にて追加分の ptnum 配列を、現在 Primitive を構成しているptnum配列の適切な位置に挿入して作り直せば完成です。

        int pts[] = primpoints(0, @primnum);
        int append_pts[] = prim(0, "rcbue__append_pts", @primnum);
        if (len(append_pts) == 0) { return; }
        // Check which edge the Point to be added is on,
        //   and add it to the position of the array
        foreach (int append_pt; append_pts)
        {
            int npts = len(pts);
            vector append_P = point(0, "P", append_pt);
            for (int i=0; i<npts; ++i)
            {
                vector pt1_P = point(0, "P", pts[i]);
                vector pt2_P = point(0, "P", pts[(i+1)%npts]);
                float dist = ptlined(pt1_P, pt2_P, append_P);
                if (dist < eps)
                {
                    insert(pts, i+1, append_pt);
                    break;
                }
            }
        }
        int add_prim = addprim(0, "poly", pts);
        removeprim(0, @primnum, 0);


ソースコードは以下にあります。
３つのステップから構成されているので構造体のメンバ関数として定義して見ました。

実際に使う場合はこんな感じになります。
Primitive Wrangle
Point Wrangle
Primitive Wrangle
の順で並びます。
それぞれの VEX コードはこうなります。

最初の Primitive Wrangle
#include "dgfx_vex_repair_utils.h"
dgfx_Repair_Crossed_Boundary_Unshared_Edges proc;
proc->Step_1st_Primitive_Wrangle(0, @primnum);

２番目の Point Wrangle 

#include "dgfx_vex_repair_utils.h"
dgfx_Repair_Crossed_Boundary_Unshared_Edges proc;
proc->Step_2nd_Point_Wrangle(0, @ptnum, @P);

３番目の Primitive Wrangle 

#include "dgfx_vex_repair_utils.h"
dgfx_Repair_Crossed_Boundary_Unshared_Edges proc;
proc->Step_3rd_Primitive_Wrangle(0, @primnum);

結果

穴が開いていた状態が…

Vertexを追加して増やす代わりに、穴を塞ぐことが出来ました。

お薬がよく効きました。それではお帰りの際にはお気をつけて、お大事になさってください。

補足：この状態の名前

T-Junction という名前で呼ばれることもあるみたいです。短くて良い名前ですね。


投稿者 時刻:
ラベル:

0 件のコメント:

コメントを投稿

登録: コメントの投稿 (Atom)